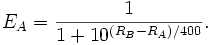 (1)
(1) Il sistema italo -
svizzero:
| Giocatori |
N° turni |
Giocatori |
N° turni |
| 9 |
3, 5 |
10 |
4 - 6 |
| 11 |
5 |
12 |
5 - 7 |
| 13 |
5, 7 |
14 |
5 - 7
(8) |
| 15 |
5, 7 |
16 |
(6) 7 -
8 (9) |
| 17 |
7, 9 |
18 |
(7) 8 -
9 (10) |
| 19 |
7, 9 |
20 |
(7) 8 -
10 (11) |
| 21 |
7, 9
(11) |
22 |
(8) 9 -
11 (12) |
| 23 |
9, 11 |
24 |
(8) 9 -
12 (13) |
| 25 |
9, 11
(13) |
26 |
(9) 10
- 13 (14) |
| 27 |
9, 11
(13) |
28 |
(9) 10
- 14 (15) |
| 29 |
11, 13
(15) |
30 |
(10) 11
- 15 (16) |
| 31 |
11, 13,
15 |
32 |
(10) 11
- 16 (17) |
Classificazione dei giocatori in base alla forza di gioco - PUNTEGGIO ELO:
il sistema ELO è un metodo usato per
calcolare il livello di forza relativo dei vari scacchisti e
predire in modo probabilistico i risultati dei loro
incontri, tornei, etc.; fu introdotto per la prima volta
dalla USCF (Federazione Scacchistica Statunitense) nel 1960, su
proposta di Arpad Elo (1903 - 1992), un fisico ed astronomo
ungherese, emigrato negli Stati Uniti in giovane età, nonchè
Maestro di Scacchi.
Il sistema è fondato su principi statistici che tentano di
misurare la "reale forza di gioco" R dei giocatori (ovviamente
incognita) e si basa sulle seguenti ipotesi: la
prestazione dei giocatori è distribuita secondo la curva normale di Gauss ed
ha la stessa deviazione
standard per ogni giocatore; tale prestazione varia
lentamente nel tempo e il suo valore più attendibile è la media
aritmetica della sua distribuzione
statistica; la prestazione può essere misurata solo dai
risultati delle partite giocate; se un giocatore ha risultati
migliori di quanto indichi il suo punteggio Elo, significa che
la sua prestazione è migliorata e di conseguenza il punteggio
deve essere aumentato (o viceversa); una differenza di 200 punti
tra due giocatori significa che il più forte dei due conquisterà
il 75% dei punti in un ipotetico "match" fra loro.
Successivi studi mostrarono che la prima ipotesi non è del tutto
corretta, in particolare per i giocatori della fascia bassa e
alta: la distribuzione statistica è piuttosto quella di una curva logistica; perciò il
sistema fu modificato in tal senso, sia dalla USCF sia dalla
FIDE (Federation International des Echecs) che lo adottò a
partire dal 1970.
Per avere un'idea di quale può essere il punteggio di un
giocatore nel sistema Elo, si consideri la seguente tabella:
| PUNTEGGIO |
LIVELLO DI GIOCO |
| meno di
1200 |
principiante |
| 1200 -
1300 |
Terza
categoria Sociale (3°S) |
| 1300 -
1400 |
Seconda
categoria Sociale (2°S) |
| 1400 -
1500 |
Prima
categoria Sociale (1°S) |
| 1500 -
1600 |
Terza
categoria Nazionale (3°N) |
| 1600 -
1800 |
Seconda
categoria Nazionale (2°N) |
| 1800 -
2000 |
Prima
categoria Nazionale (1°N) |
| 2000 -
2200 |
Candidato
Maestro (CM) |
| 2200 -
2300 |
Maestro
Nazionale (M°) |
| 2300 -
2400 |
Maestro
FIDE (FM) |
| 2400 -
2500 |
Maestro
Internazionale (IM) |
| 2500 -
2700 |
Gran
Maestro (GM) |
| 2700 + |
Super -
GM (livello del Campione del Mondo) |
A
tutt'oggi (dicembre 2015) solo 9 persone (Magnus Carlsen, Garry
Kasparov, Fabiano Caruana, Levon Aronian, Viswanathan Anand,
Veselin Topalov, Hikaru Nakamura, Vladimir Kramnik e Alexander
Grischuk) hanno mai raggiunto un punteggio superiore a 2800
punti (il punteggio più alto di Bobby Fischer fu 2785, quello di
Karpov 2780). Il punteggio più alto mai ottenuto nella storia è
stato conseguito da Carlsen (attuale Campione del Mondo) con
2882 punti (nel maggio 2014); seguono Kasparov con 2851, Caruana con 2844, Aronian con 2830, Anand con 2817,
Topalov con 2816, Nakamura con 2814, Kramnik con 2811 e Grischuk
con 2810. Attualmente solo 2 giocatori (a parte Kasparov, che
quando si è ritirato aveva 2812) hanno un punteggio superiore o
uguale a 2800 punti (Carlsen, il primo della lista corrente, ha
2834 punti Elo al dicembre 2015 e Topalov 2803).
In tutta la storia della FIDE, solo 98 giocatori hanno raggiunto
o superato nella loro vita 2700 punti (vedi https://en.wikipedia.org/wiki/List_of_chess_players_by_peak_FIDE_rating).
Il rating più alto mai ottenuto da un giocatore italiano è 2844
di Fabiano Caruana (nel ottobre 2014), il cui punteggio attuale
è 2787, che corrisponde al 7° rating del mondo. Il rating
più alto ottenuto da una donna è 2735 di Judit Polgar, ottenuto
nel luglio 2005. Questi sono tutti rating ufficiali della FIDE (http://www.fide.com/), la
quale da alcuni anni pubblica anche i rating "rapid" e "blitz".
Esiste poi anche un "Live rating", che viene aggiornato dopo
ogni incontro (vedi l'ottimo e ricco sito http://2700chess.com/). I
rating "live" piú alti della storia sono in genere di poco
superiori a quelli ufficiali FIDE. Per esempio il "peak live
rating" di Carlsen é 2889,2 dell'aprile 2014.
Ad un nuovo giocatore, precedentemente inclassificato, viene
solitamente attribuito il punteggio convenzionale di 1400
(insieme ad un'elevata varianza
K, vedi oltre). In occasione di acquisizione di un titolo
riconosciuto dalla FIDE (es. Maestro Fide) il punteggio viene
aggiornato (se inferiore al minimo della categoria), per
riflettere più correttamente la nuova situazione.
il punteggio atteso EA di un
giocatore A, in un dato incontro con un altro giocatore B, è dato
dalla speranza matematica di
quel giocatore, ovvero la somma della probabilità che A vinca
l'incontro più la metà della probabilità che l'incontro termini in
parità (perchè la "patta" vale 1/2 punto a testa, cioè è
considerata come una mezza vittoria più una mezza sconfitta). Tale
probabilità si potrebbe calcolare esattamente (nell'ipotesi che le
distribuzioni statistiche delle prestazioni seguano una curva logistica) se fosse
nota la "forza reale" dei due giocatori. Siccome tali dati sono
invece incogniti, essi vengono stimati in base ai punteggi ("rating")
ELO attuali, RA ed RB rispettivamente. In tal caso
la formula per trovare il punteggio atteso per il giocatore A è:
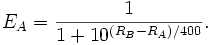 (1)
(1)
Analogamente la formula per trovare
il punteggio atteso per il giocatore avversario B è:
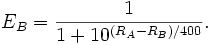 (2)
(2)
Si noti che la somma dei due valori
EA ed EB fa 1, come dovrebbe essere ovvio.
Se un giocatore ottiene un punteggio ("score") reale SA, diverso dal punteggio atteso, significa che il
suo "rating" deve essere aggiornato (in aumento se SA
> EA e in diminuizione se SA < EA).
Indicando con K la massima possibile variazione
per partita, il nuovo punteggio R'A è dato
dalla semplice formula lineare:
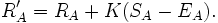 (3)
(3)
in cui eventuali valori decimali
vengono approssimati per difetto o per eccesso alla cifra intera.
Questo "aggiornamento" può essere fatto (ufficialmente) dopo ogni
torneo o addirittura dopo ogni incontro, ovvero dopo un certo
periodo di tempo (la FIDE ad esempio aggiorna ufficialmente i
punteggi ELO ogni due mesi). In ogni caso all'interno dello stesso
periodo di validità dei punteggi, i cambiamenti sono additivi. Un esempio chiarirà
la cosa nel modo migliore:
supponiamo che un giocatore A di una
certa esperienza di gioco (per il quale ad es. K = 30) abbia un
punteggio RA = 1613 e giochi in un torneo avente 5
turni. Nel 1° turno perda con un giocatore avente 1609 punti, nel
2° turno patti con un giocatore da 1477 punti, poi vinca con un
giocatore da 1388, e successivamente vinca contro un giocatore da
1586; infine perda con un giocatore classificato 1720. Il suo
punteggio finale sarà di 2,5 punti su 5 totali. Calcolando il suo
punteggio atteso totale usando cinque volte la formula (1) si
ottiene:
EA = 0,506 + 0,686 + 0,785 + 0,539 + 0,351 = 2,867.
In base a ciò, il suo nuovo punteggio sarà:
R'A = 1613 + 30 · (2,5 - 2,867) = 1613 - 11,01 =
1601,99 --> 1602
Il punteggio diminuisce lievemente perchè il giocatore A ha avuto
una prestazione lievemente inferiore a quanto ci si sarebbe potuti
attendere da lui, dato che ha incontrato un punteggio medio avversario
RM pari a:
RM = (1609 + 1477 + 1388 + 1586 + 1720) / 5 = 1556
e quindi inferiore al suo. Se fosse riuscito a pattare una delle
due partite che ha perso (ad es. al primo turno) e quindi a
conseguire 3 punti in totale, il suo nuovo punteggio sarebbe stato
invece:
R'A = 1613 + 30 · (3 - 2,867) = 1613 + 3,99 = 1616,99
--> 1617
perchè avrebbe fatto una prestazione di poco superiore a quanto ci
si sarebbe potuti attendere da lui.
Di particolare importanza nella
formula (3) è il valore del parametro K che viene utilizzato: un
valore troppo basso rende i punteggi ELO troppo "conservativi",
mentre un valore troppo alto può produrre un sistema troppo
caotico. D'altra parte quando un giocatore viene classificato per
la prima volta, il suo punteggio provvisorio può essere anche
molto lontano dal valore vero e quindi è opportuno che i suoi
aggiornamenti di punteggio vengano calcolati con un valore K
abbastanza alto, onde favorire la convergenza verso il valore
reale.
La FIDE adotta un sistema basato sulla seguente tabella:
| Caratteristiche giocatore |
parametro K |
| meno di 30 partite valutate;
con qualunque rating |
45 |
| 30 o + partite; rating <
2000 |
30 |
| 30 o + partite; 2000
<= rating < 2400 |
130 -
rating / 20 |
| 30 o + partite; rating 2400 o
+ |
10 |
dove la formula che permette di
ottenere K nella terza riga, va valutata considerando
l'approssimazione al valore intero più vicino (in altre parole non
si ammettono valori frazionari di K).
Tale sistema per determinare K è comunque in parte soggetto a
critiche; ad esempio l'esperto di statistiche scacchistiche Jeff
Sonas ritiene che il valore 10 usato per gli scacchisti più forti,
sia un valore troppo piccolo e riterrebbe invece più accurato
l'uso di un parametro K pari a 24. La USCF utilizza K = 32 per i
giocatori meno forti e K = 16 per i più forti (da Maestro in su).
Siti web che offrono modalità di gioco "on-line" usano vari
sistemi diversi tra loro, a seconda del numero di partite giocate
o del rating.
Sono anche stati proposti sistemi che premiano i giocatori più
attivi (con una certa frequenza di partite classificate in un
certo arco di tempo) e puniscono quelli meno attivi.
Si noti inoltre che in ogni caso vanno escluse dal computo Elo le
partite perse per forfait, simultanee, alla cieca, dimostrative, a
tema e a tempo ridotto (lampo o semi-lampo). Per quest'ultimo tipo
di partite sono stati introdotti punteggi Elo a parte (come fanno
anche molti siti internet di gioco on-line).
Un rating alternativo che sembra molto interessante é il sistema
Glicko (http://www.glicko.net/glicko.html).
Esso viene usato anche dall'ottimo sito di gioco on-line Lichess (http://en.lichess.org/ o in
italiano http://it.lichess.org/)
Infine si può accennare al fatto che
negli ultimi anni, soprattutto per i Tornei Internazionali ad
altissimo livello, si tende a fornire anche una stima della prestazione ELO di ogni singolo
partecipante, da confrontare con il rispettivo punteggio ELO. Tale
prestazione non va confusa con la variazione effettiva del
punteggio ELO del giocatore (ottenuta in base alla formula (3) per
intenderci) in seguito ai risultati ottenuti. La prestazione
rappresenta invece il punteggio ELO che dovrebbe avere un
giocatore per avere un punteggio atteso pari ai punti effettivi
che ha ottenuto il reale giocatore considerato in quel torneo (e
contro quegli avversari). Chiaramente se i punti ottenuti
coincidono con i punti attesi, la prestazione coincide con il
reale punteggio ELO del giocatore considerato. In caso contrario,
vi sono vari metodi di stimare la prestazione.
La stima più naturale (e più usata nella pratica) può essere fatta
in base alla stessa curva con cui viene calcolato il punteggio
atteso, cioè la curva logistica; se p% indica la percentuale di punti
ottenuti sul totale di punti disponibili (n° delle
partite giocate), si ha:
Perf = RM + 400 · Log10 [ p% / ( 100 - p% ) ] (4)
Ciò dovrebbe produrre un risultato
più realistico nella maggior parte dei casi concreti; tuttavia
cade in difetto nel caso che un giocatore vinca tutte le partite
(in cui la sua prestazione verrebbe considerata pari ad infinito!)
o nel caso che al contrario perda tutti gli incontri (in cui la
sua prestazione verrebbe considerata pari a meno infinito!!). In
entrambi questi casi limite, la valutazione non sarebbe quindi
affatto realistica.
Per ovviare a ciò Jeff Sonas propone nel suo sito (http://chessmetrics.com/cm/)
una semplice interpolazione
lineare
Perf = RM + [ ( p% - 50) · 8,5 ] (5)
basata sulla sua esperienza
statistica e che ha il vantaggio di avvicinarsi di molto alla
curva logistica nella parte centrale, oltrechè evitare le
situazioni singolari presentate precedentemente.
Ad es. nel caso dell'esempio suesposto, relativo al giocatore di
punteggio 1613 (nell'ipotesi iniziale di 2 vittorie, 2 sconfitte e
1 patta), la prestazione valutata, sia secondo la formula (4) che
secondo la formula (5), sarebbe pari al punteggio medio degli
avversari, cioè 1556. Nella seconda ipotesi invece (2 vittorie, 1
sconfitta e 2 patte), la formula (4) fornirebbe 1626 punti
(approssimando alla parte intera) e la formula (5) darebbe invece
una prestazione da 1641 punti. Si tratta comunque di una
differenza non grande.
Le cose sarebbero andate diversamente se il giocatore dell'esempio
fosse riuscito a vincere tutte le cinque partite (evento
improbabile ma non impossibile), nel qual caso il suo nuovo
punteggio Elo sarebbe diventato 1677, la sua prestazione sarebbe
stata valutata pari a 1981 secondo la formula (5) e, poco
realisticamente, pari a infinito in base alla (4).
Un metodo che unisce i pregi di entrambi, per quanto più
complesso, potrebbe essere quello di utilizzare la formula (4) nel
più comune intervallo centrale (p% che va da 15,79 % a
84,21 % - valori in corrispondenza ai quali le due linee si
intersecano) e la formula (5) negli intervalli esterni (meno del
15,79 % o più del 84,21 %).